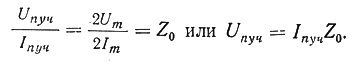HAMLOG
Скачать
Программы
Схемы, статьи
Наш форум
Доска объявлений
Фотоальбомы
Гостевая
Обратная связь
Волгоград
Начинающему
Музей
Лирика Радио
Ham юмор
DX-монитор
OPDX бюллетень
Календарь соревнований
Проверь свою eQSL почту
HAM карты
Карта высот
Найди свой QTH-Loc
Каталог сайтов
FAQ (как добавить материал?)
Правила пользования сервисом
Микропроцессоры
Микропроцессоры
Литература
Другие
Всё остальное
| Главная » Статьи » Статьи |
Добавить статью |
|
ЛИНИИ ПЕРЕДАЧИ И СТОЯЧИЕ ВОЛНЫ В. Костычев, UN8CB г. Петропавловск. Казахстан.
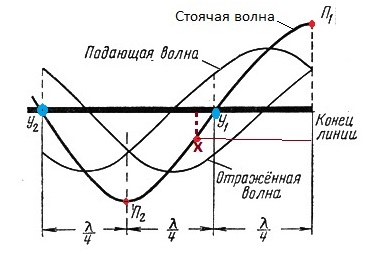
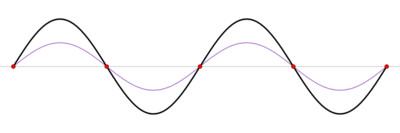
Линии передачи по своим параметрам аналогичны колебательным контурам, но в отличие от них параметры линии передачи (L - индуктивность проводников, C- ёмкость между проводниками, R - активное сопротивление проводников, G- проводимость диэлектрика линии) не являются сосредоточенными, а равномерно распределены по всей длине линии. Параметры L и С характеризуют резонансные свойства линии, а параметры R и G характеризуют потери (затухание) в ней. В зависимости от характера и величины сопротивления нагрузки линии, линия передачи может работать в режимах бегущей волны, стоячей волны или в смешанном режиме. Режим бегущей волны возникает, когда сопротивление нагрузки Zn и волновое сопротивление линии Zo равны и отражения от конца линии не возникает. Стоячие волны возникают в линии передачи, если её волновое сопротивление Zo не равно сопротивлению нагрузки Zn. Рассмотрим сначала предельные ситуации в линии передачи, когда линия разомкнута либо замкнута накоротко. Если линия на конце замкнута накоротко (Zn =0) или разомкнута ( Zn = бесконечности), то вся поступающая энергия отражается от конца линии и возвращается ко входу. Рассмотрим случай, когда линия разомкнута на конце, т. е. когда нагрузочное сопротивление бесконечно велико. Бегущая волна, дойдя до конца разомкнутой линии, отражается и двигается обратно к генератору. Таким образом, в линии распространяются две бегущие волны: одна — падающая — движется от генератора к концу линии, а другая — отраженная — движется в обратном направлении. В результате взаимодействия падающих и отражённых волн в линии образуются стоячие волны. Эти волны проявляются наличием в линии максимумов (пучностей) напряжения и тока, а также их нулевых значений (узлов), сдвинутых по фазе относительно друг друга. На рис.1 показано сложение падающей и отраженной волн напряжения, для некоторого момента времени, в разомкнутой линии.
Рис.1 - Сложение падающей и отраженных волн
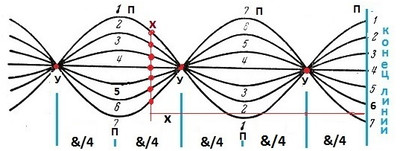
Здесь П1, П2 – пучности напряжения, У1, У2 – узлы напряжения, Х- любая точка волны на расстоянии Х от конца линии. Аналогично получается график и для стоячей волны тока, но пучности тока в ней сдвинуты на 90* относительно пучностей напряжения. Значения напряжения стоячей волны в каждой точке Х от конца линии определяется уравнением: u =2Um Cos 2πx/λ Cos ωt. И соответственно для волны тока: i = 2Im Sin2πx/λ Sin ωt. Здесь Um, Im - амплитуды напряжения и тока бегущей либо отражённой волны. Эти уравнения называют уравнениями стоячей волны. Из этих уравнений видно, что в каждой точке стоячей волны и напряжения, и тока происходят колебания и напряжения, и тока той же частоты, что и в падающих и отражённых волнах. Причём, если зафиксировать некоторую точку, которая имеет координату Х, то для значения напряжения или тока в этой точке получим уравнение колебания амплитуды напряжения или тока: Ux = |2Um Cos 2πx/λ|; Ix =|2 Im Sin2πx/λ|. Отсюда видно, амплитуда напряжения и тока стоячей волны зависит от координаты Х. Знак модуля означает, что значение амплитуды – всегда положительно. Как возникает стоячая волна и что она из себя представляет, можно наглядно проследить кликнув по картинке: Стоячая волна (чёрная линия ), возникает в результате сложения двух волн, падающей и отражённой (красная и синяя линии), распространяющихся во встречных направлениях. Красные точки обозначают узлы — точки или области в пространстве, в которых амплитуда колебательного процесса минимальна и равна разности амплитуд падающей и отражённой волн (амплитуда стоячей волны в узлах равна нулю). Посередине между каждой парой соседних узлов располагается пучность — точка или область в пространстве, в которой амплитуда стоячей волны максимальна и равна сумме амплитуд падающей и отражённой волн. Фаза колебательного процесса стоячей волны при переходе через узел меняется на 180°. Характер распределения напряжения или тока вдоль линии при стоячей волне не изменяется с течением времени. В разные моменты времени изменяется только величина напряжения или тока в каждой точке линии. На рис.2 показано распределение напряжения вдоль разомкнутой линии для нескольких различных моментов времени на протяжении нескольких полупериодов. Рис.2 - Распределение напряжения вдоль линии при стоячей волне для разных моментов времени (П – пучности напряжения , У - узлы напряжения). Кривая 1 соответствует фазе, когда напряжение в линии наибольшее. Далее напряжение становится всё меньше и меньше (кривые 2 и 3). Затем напряжение во всей линии становится равным нулю (прямая 4). Затем оно меняет знак и начинает возрастать (кривые 5 и 6). Через полпериода после начала процесса напряжение снова достигает амплитудного значения (кривая 7), но с обратным знаком. В каждой точке Х линии напряжение колеблется по синусоидальному закону, причем мгновенные значения напряжения этого колебания (амплитуды для этих точек) для разных точек различны. Для пучностей амплитуда наибольшая, равная двойной амплитуде бегущей волны, для других точек она меньше, и, наконец, для узлов она равна нулю.
Рис.3 - Изображение стоячих волн тока и напряжения в линии
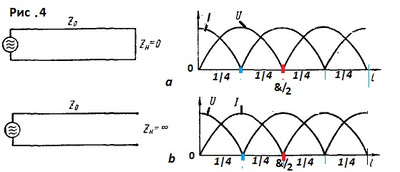
Так как амплитуды напряжения и тока в стоячей волне величины положительные, на графиках часто их откладывают в положительной области. На рис.4 представлены графики распределения напряжения и тока стоячих волн в короткозамкнутой линии (рис.4а) и разомкнутой линии (рис.4б)
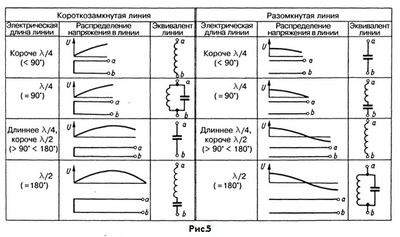
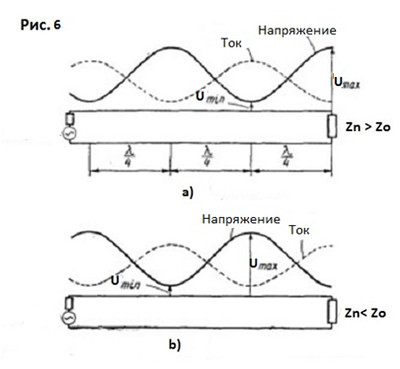
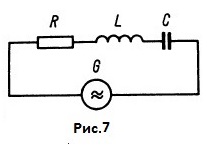
В каждом случае сопротивление, как в каждой точке линии, так и на её концах, определяется отношением напряжения к току – U/I. Вследствие разности фаз между током и напряжением, линия передачи характеризуется не только активным сопротивлением, но и реактивным, которое может быть индуктивным (XL) или емкостным ( Xc) в зависимости от знака фазового сдвига . Сдвиг фаз на 90° между током и напряжением при стоячей волне показывает, что в линии происходит колебание энергии, сходное с колебательным процессом в замкнутом контуре. Когда напряжение в линии наибольшее, а ток равен нулю, то вся энергия сосредоточена в электрическом поле. Через четверть периода напряжение равно нулю, а ток имеет наибольшее значение и вся энергия сосредоточена в магнитном поле. Еще через четверть периода энергия снова возвратится в электрическое поле и процесс колебания энергии повторится. На рис.4а по графику видно, что на конце линии, замкнутой накоротко, (начало координат) ток имеет максимальное значение (пучность тока), а напряжение равно нулю, т.к. сопротивление нагрузки равно нулю (Zn=0). Начиная же с закороченного конца линии начинает возрастать индуктивная составляющая импеданса - XL, которая достигает наибольшего значения на расстоянии 1/4 & (&-лямбда) от конца линии. Но здесь ей противостоит столь же большая емкостная составляющая импеданса - Xc, возникающая в следующем участке 1\4 & длины линии. На расстоянии &/4 от конца закороченной линии, линия представляет собой параллельный контур, а параллельно включенные индуктивная и емкостная составляющие импеданса равны (XL= Xc), и полное сопротивление линии в этой точке становится чисто активным. На отрезке линии между &/4 и &/2 емкостная составляющая импеданса уменьшается до нуля и в точке &/2 импеданс снова становится чисто активным. В этой точке линия представляет собой последовательный колебательный контур. Далее ход импеданса повторяется и в зависимости от своей длины короткозамкнутая двухпроводная линия передачи (фидер) настраивается или как индуктивность, или как емкость подобно последовательному либо параллельному резонансному контуру. Сходным образом ведёт себя и разомкнутая двухпроводная линия. Рис.4b. В этом случае соотношения импеданса сдвинуты на 90 градусов относительно короткозамкнутого режима (рис.4а). Открытому концу линии (на графике начало координат) соответствует бесконечно большое емкостное сопротивление, спадающее до нуля через 1/4 & длины линии. В этой точке линия ведёт себя как последовательный резонансный контур с чисто активным полным сопротивлением. Между точками &/4 и &/2 импеданс носит индуктивный характер, а при &/2 устанавливается режим параллельного резонанса и т.д. Эти свойства двухпроводной линии (фидера) позволяют использовать их как резонансные элементы в колебательных контурах, фильтрах, согласующих устройствах и пр. Отрезки линии, представляющие собой эквиваленты индуктивности, ёмкости или колебательного контура, могут иметь длину менее &/4. Это позволяет подбором длины линии получить необходимую индуктивность или ёмкость. Например, нужную индуктивность можно получить из короткозамкнутой линии длиной меньше &/4, а из разомкнутой линии длиной менее &/4 можно получить необходимую ёмкость. Замкнутая линия длиной &/4 представляет собой параллельный колебательный контур, а эта же разомкнутая линия превратится в последовательный колебательный контур. На рис.5 представлены разные возможности использования короткозамкнутой или разомкнутой линии в качестве согласующего элемента. Холостой ход (линия разомкнута) и короткое замыкание являются предельными ситуациями в линии передачи. Когда сопротивление нагрузки линии Zn больше нуля или меньше бесконечности, но не равно волновому сопротивлению линии Zo, падающая волна частично отражается от конца линии и в ней устанавливается режим смешанных волн, но амплитуда отражённой волны будет меньше, чем в случае короткозамкнутой или разомкнутой линии. В случае, когда сопротивление нагрузки Zn больше Zo, напряжение максимально на нагрузке и в точках, отстоящих от конца линии на кратное число полуволн, как и в случае линии, разомкнутой на конце. В тех же самых точках будут минимумы тока, а максимумы тока находятся в точках, отстоящих от конца линии на нечетное число четвертей волн, рис. 6a. Если же Zn < Zo, максимумы напряжения будут находиться, как и в замкнутой линии, в точках, отстоящих от конца линии на нечетное число четвертей волн, в тех же точках будут минимумы тока, рис. 6b. Линии передачи могут быть как произвольной длины (не настроенные), так и настроенные. Линию передачи называют настроенной, если её электрическая длина равна нечётному числу четвертей волн (четвертьволновый трансформатор) или целому числу полуволн (полуволновый повторитель). Несмотря на наличие стоячих волн в таких настроенных линиях, их входные и полные выходные сопротивления являются активными (чисто омическими), они являются только переносчиками импеданса и не влияют на резонансную частоту антенны. Настроенную линию передачи допустимо рассматривать как неизлучающее продолжение антенны. Если же линия передачи не настроенная (произвольной длины) и Z n не равно Zo (несогласованная), в линии наряду с бегущими волнами возникают стоячие волны (смешанный режим), появляется реактивность, которая может быть индуктивной (XL) или емкостной ( Xc) в зависимости от длины линии (знака фазового сдвига между током и напряжением ). Антенна, как и линия передачи, так же представляет собой резонансный контур с распределёнными параметрами. Рис.7.
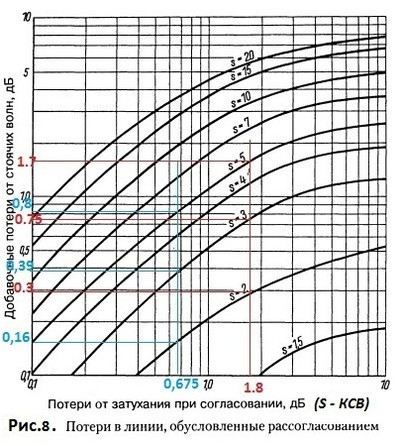
Распрямлённый проводник также обладает индуктивностью и ёмкостью, которые распределены по всей его длине. Когда проводник находится в резонансе с возбуждающей частотой, его можно рассматривать как колебательный контур. К примеру, эквивалентная схема полуволнового вибратора представляет собой последовательный резонансный контур. Рис.7. Несогласованные линии передачи произвольной длины, вследствие возникновения в них стоячих волн, добавляют реактивность в антенную систему антенна-фидер, резонансная частота которой может быть сдвинута вверх или вниз по частоте, в зависимости от знака реактивности (XL или Xc) на конце линии, подключаемой к антенне. Линии передачи, работающие в режиме стоячей волны, имеют бОльшие потери, чем линии, работающие в режиме бегущей волны. Это объясняется тем, что в режиме стоячей волны в пучностях тока увеличиваются омические потери в проводниках, а в пучностях напряжения увеличиваются диэлектрические потери в диэлектрике линии передачи. Рассмотрим, как влияет рассогласование линии передачи (фидера) с антенной вследствие возникновения стоячих волн на добавочные потери мощности. Расчитаем потери в линии передачи на конкретном примере. Согласно справочным данным, для кабеля RG-58 C/U (диаметр 5 мм) затухание на частоте 21 МГц составляет 0,06 дБ/м. Если линия передачи согласована, стоячие волны отсутствуют, то суммарные потери этого кабеля длиной 30 м составят: 30 Х 0,06 = 1,8 дБ. Если линия передачи не согласована , то в линии, за счёт возникновения стоячих волн, появятся добавочные потери, величину которых можно определить из графика рис.8. Для нашего случая при погонном затухании всего кабеля - 1,8 дБ, добавочные потери составят: для КСВ=2 – 0.3 дБ; для КСВ=3 – 0,75 дБ; для КСВ=5 – 1,7 дБ. Или в сумме: для КСВ=2 – 2,1 дБ; для КСВ=3 – 2,55 дБ; для КСВ=5 - 3,5 дБ. Такие же потери будут в кабеле RG-213/U (диаметр 10 мм) длиной 45 м, но на частоте 30 МГц (затухание 0,04 дБ/м на частоте 30МГц). А этот же кабель на частоте 5 МГц (затухание 0.015 дБ/м на частоте 5 МГц) длиной 45 м будет иметь затухание: 45 х 0,015 = 0,675 дБ. Добавочные потери составят: для КСВ=2 - 0,16дБ; для КСВ=3 – 0,35 дБ; для КСВ=5 – 0,8дБ. Или в сумме: для КСВ=2 – 0,835 дБ; для КСВ=3 - 1,065 дБ; для КСВ=5 - 1,475 дБ. Потери в двухпроводных воздушных линиях на порядок меньше. Точнее потери в линиях можно рассчитать используя программу TLDetails.
Так для того же кабеля RG-58 C/U длиной 30 м на частоте 21 МГц TLDetails выдаёт: - для КСВ = 1 потери 1,988 дБ, или 36,7 Вт при подводимой мощности 100 Вт; - для КСВ = 2 потери 2,28 дБ или 40,9 Вт; - для КСВ = 3 потери 2,75 дБ или 46,9 Вт. Для кабеля RG-213/U длиной 45 м на частоте 3,6 МГц: - для КСВ =1 потери 0,534 дБ или 11,5 Вт; - для КСВ = 2 потери 0,673 дБ или 14.3 Вт; - для КСВ = 3 потери 0,876 дБ или 18,3 Вт.
Литература: 1.К.Ротхаммель, Изд. 11 .Т.1, гл.5. 2.С.Г.Бунин, Л.П. Яйленко. Справочник радиолюбителя - коротковолновика. Киев. 1984
В. Костычев, UN8CB г. Петропавловск. Казахстан. | |
| Просмотров: 7531 | Теги: | Рейтинг: 3.7/3 |
| Всего комментариев: 0 | |